One’s Place
May 18 - June 23, 2024 at Soft Serve Projects in Ridgewood, Queens. One’s Place is a performance series dealing in elementary math and the language of numbers. See press release by Violet Saxon here. Documentation by Matthew Xavier Praley.






 Installation view
Installation view Installation view
Installation view

Hundred Chart, graphite and colored pencil on rice paper, 2024
 One’s Place, ink on paper, 2024
One’s Place, ink on paper, 2024 Multiples of 2, 3, 4, 5, 6, 7, 8, and 9, graphite and colored pencil on graph paper, 2023-24
Multiples of 2, 3, 4, 5, 6, 7, 8, and 9, graphite and colored pencil on graph paper, 2023-24
 Counting to One Hundred on My Hands, ink on legal paper, 2023
Counting to One Hundred on My Hands, ink on legal paper, 2023

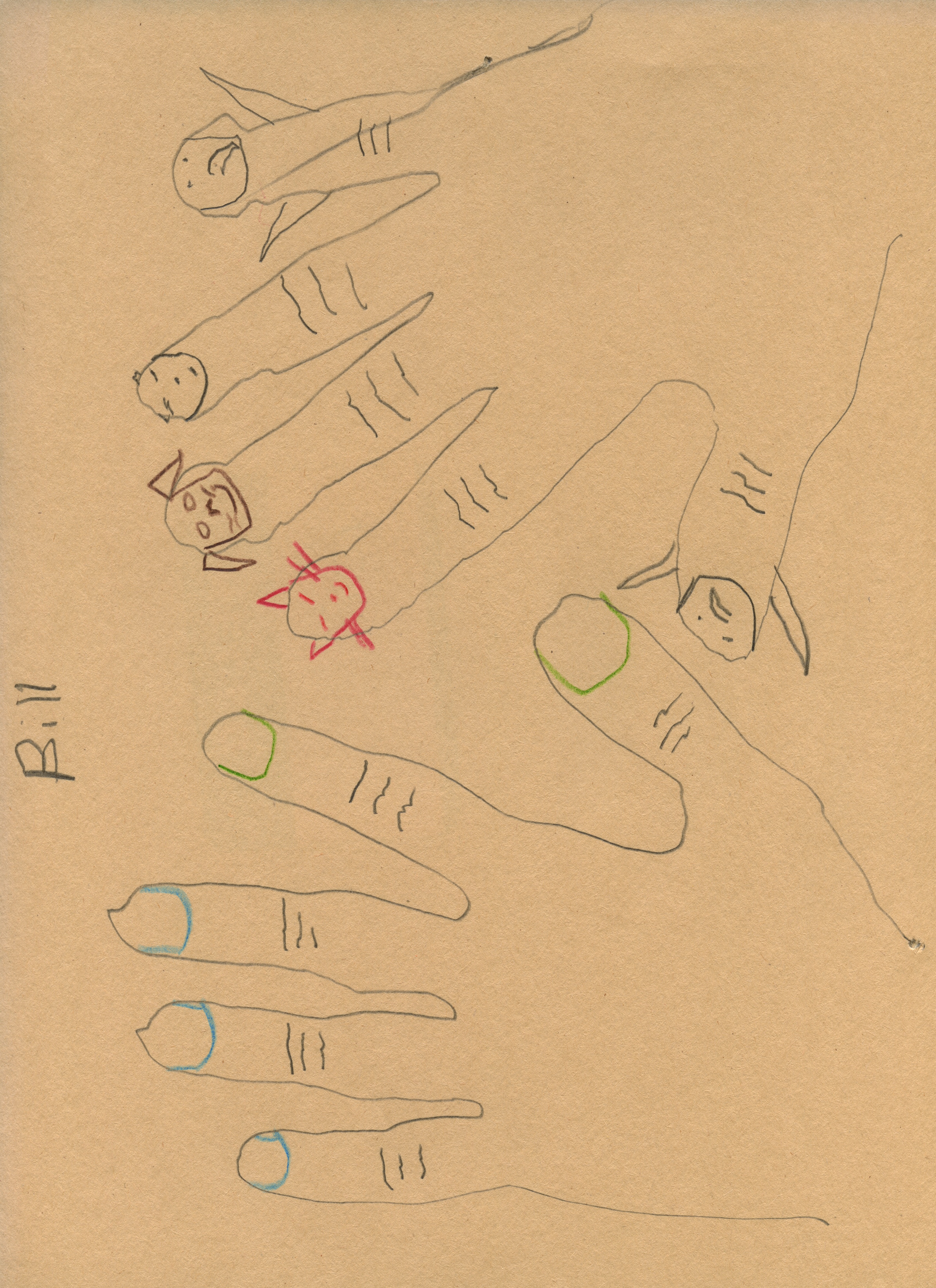
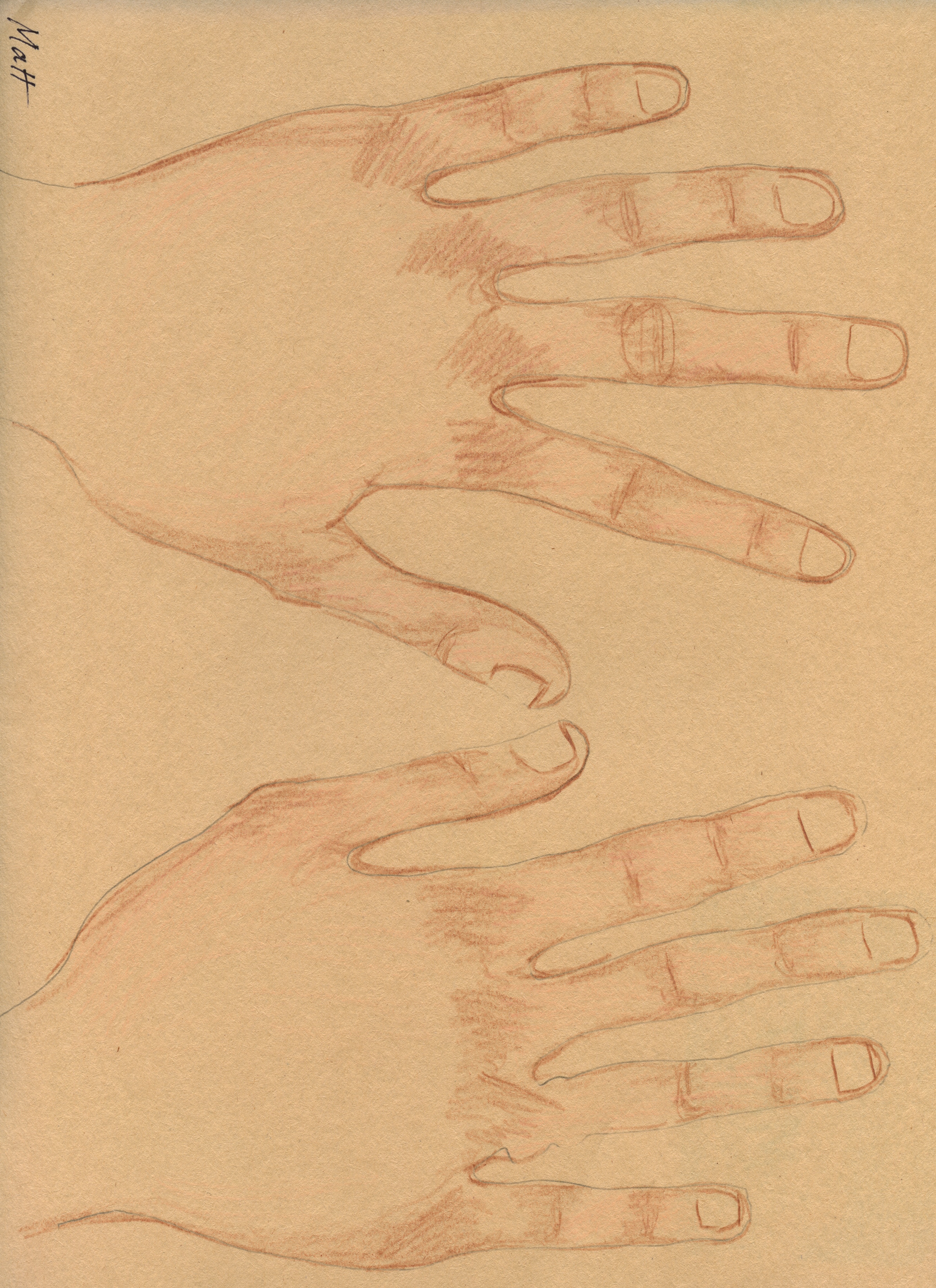


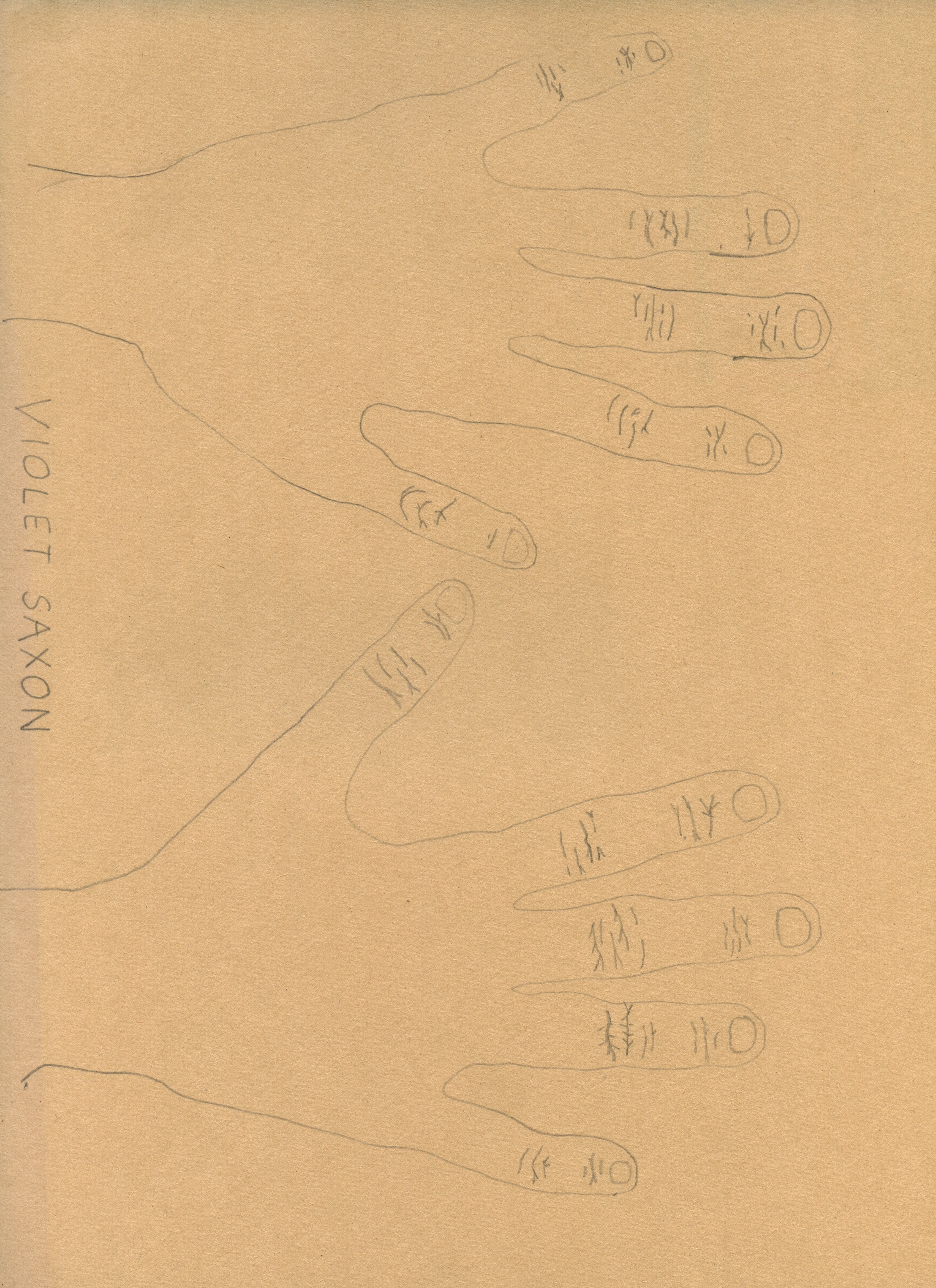
At the beginning of each lesson, participants traced their hands. The hands were decorated as people listened and shared about their changing relationships to the language of numbers.



Before children learn the four basic operations, they learn how to count by ones: 1, 2, 3, 4, 5, 6, 7 and so on. Counting to 100 feels like touching the sky.
“I can count to 100.”
“I can count to 200.”
“I can count to 1,000.”
“Well, I can count to 1,000,000.”
“No, you can’t.”
“Yes, I can.”
“No, even if you counted all day you would fall asleep first.”
Numbers expand into infinity, the unreachable, the forever counting. To get there faster you skip-count.
Skip-counting by 10s comes easily: You hold up both hands and flash all your fingers over and over again. 10, 20, 30, 40, 50, 60, 70, you and your classmates count in chorus. When you get to 100 you either pause as if there’s a comma, or stop.
Next you’ll skip-count by twos. Twos are pairs—they make even number after even number. What’s an even number? You just found out. Humans are organized in pairs—our two eyes, two ears, two arms, two legs.
Then fives. Skip-counting by fives just feels like sneaking in an extra between each multiple of 10. 10, 15, 20. It’s doable, and the rhythm of making a stop before stating the next 10 is easy to find.
Threes come next. With the introduction of skip-counting by threes, you start to see how the repeated addition of these numbers forms a certain shape and feeling. 3s are an arrow to some children, pointing in a curious direction. To others they feel like a trick. What to do with 3s? Do we think in 3s? Later, you learn that 1/3 can’t be written as a finite decimal number, only as 0.3333333333333333(forever). Maybe this speaks to the oddness of threes. Halves versus thirds. If they can stand it, it does someone a lot of good to really sit with thirds – learn how to draw them, learn how to feel them.
When children get older, they’ll refer to these sets of skip-counted numbers as “multiples” of 2, 3, 5, 10. They’ll learn their multiplication facts. Skip-counting— pathfinding towards infinity—solidifies into facts.
In One’s Place, we’ll look at how we use the language of numbers in our lives, pathfinding toward the big 100.